| Documentation: | Online | PDF |
| Development sources: | GMP repository - Repo usage tips | Daily snapshots |
| Testing: | Head status | All status | Head coverage |
| Speed: | Performance guard |
| Tuneup: | Current threshold tables |
| Asm: | Assembly loops | Performance anomalies |
| Computers: | GMP developer's systems |
| Incompatibility: | Incompatible changes considered |
GMP release update
GMP 6.3.0 is out 2023-07-30.
GMP itemised plans
List of planned GMP improvements
List of desirable ARM improvements
List of desirable X86-64 improvements
List of desirable SPARC (T4-T5) improvements
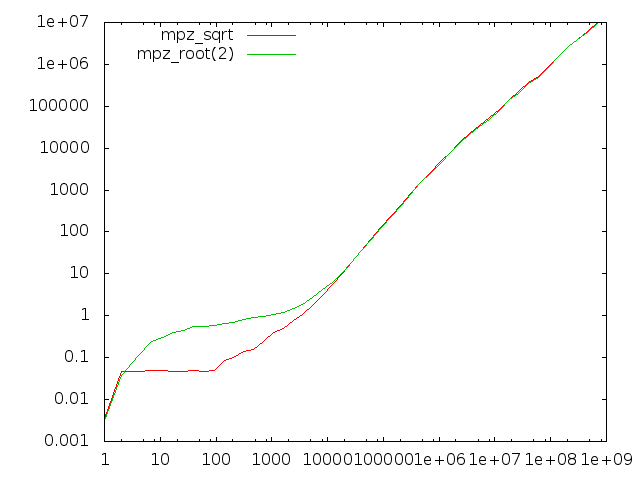
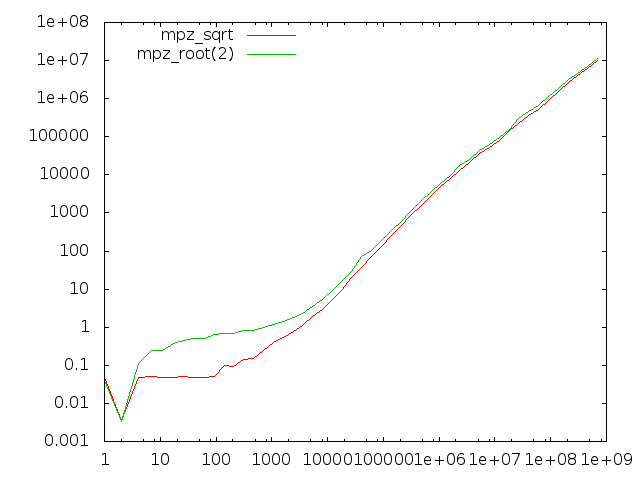
Comparing sqrt and root(2)
We use quite different algorithms for mpz_sqrt/mpz_sqrtrem/mpn_sqrtrem and mpz_root/mpz_rootrem/mpn_rootrem. Here we compare the former group to the latter group for computing square roots.
The x-axis represents input operand size in bits. The left-hand diagram is for computing just the root result, the right-hand diagram also computes the remainder.
There are two anomalies here, one very visible and one quite subtle:
- The root functions badly underperform for operands of less than about 10000 bits; this is due to the absence of starting value tables for the Newton code and that sqrt has register-based code for the first few iterations.
- When producing the remainder, the root functions perform about 20% worse than the sqrt functions.
- Less visible is that for quite large operands the sqrt function performs around 5% worse than the more general root function when both are asked not to return the remainder. This is supposedly related to the different strategies of the sqrt and root code; the former basically computes a remainder always in order to adjust the final result, the latter computes an extra limb which usually allows it to return the accurate result without further work.
|
|
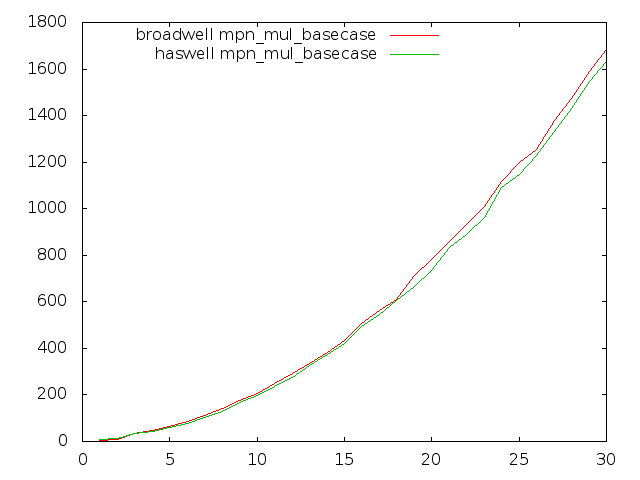
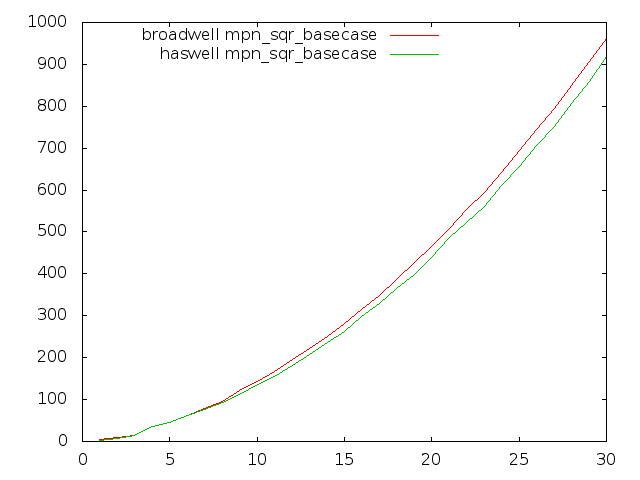
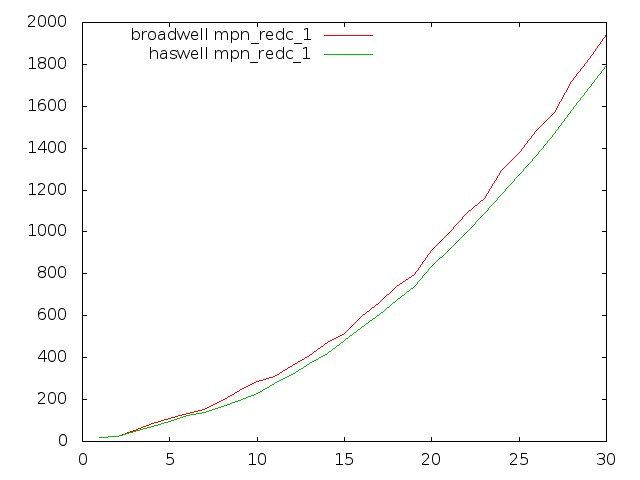
Broadwell optimisation
Most GMP's inner-loops run faster on Broadwell than on Haswell in GMP 6.0.0, but unfortunately some of the most critical multiply loops run quite considerably slower.
These plots compare Haswell and Broadwell using the dev sources for plain multiplication, squaring, and Hensel remaindering. Dimension is cycles per n-limb operands, meaning that lower is better.
|
|
|
Basecase performance (obsolete with 6.0.0)
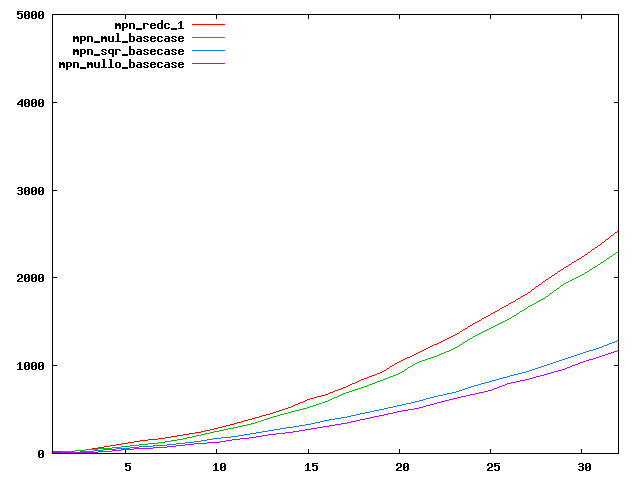
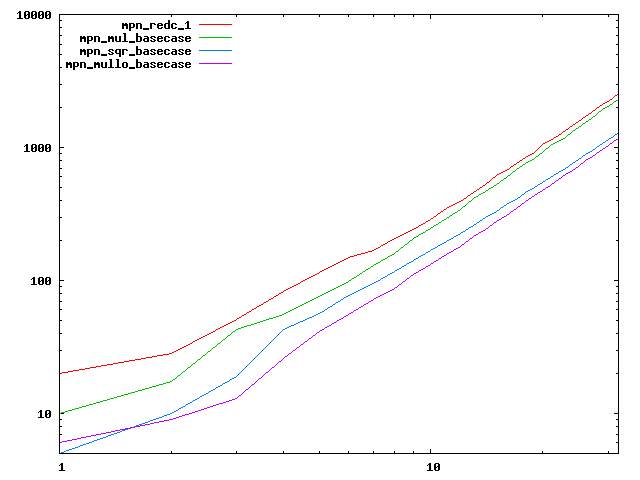
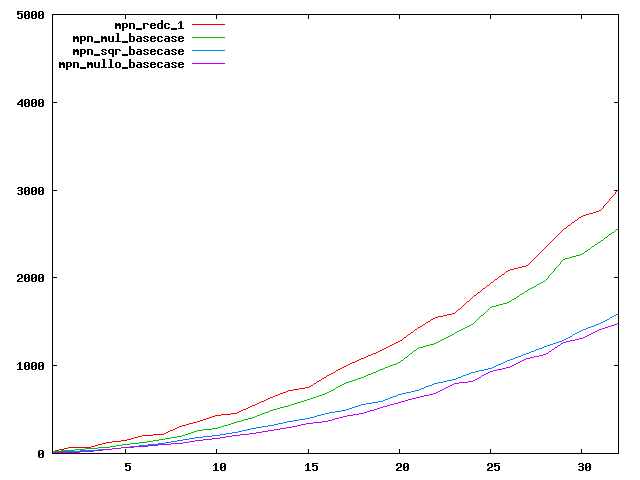
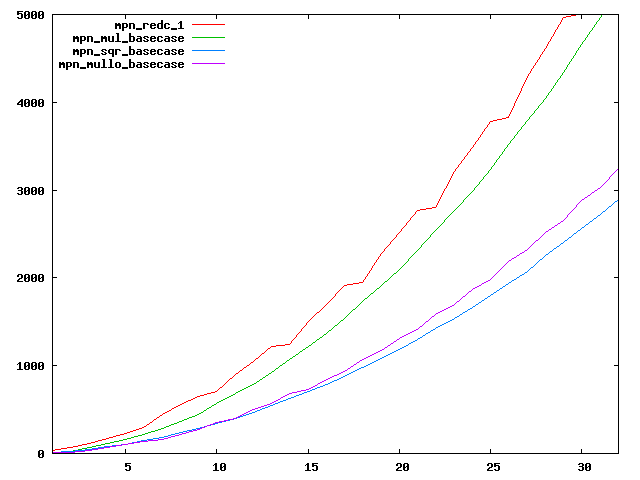
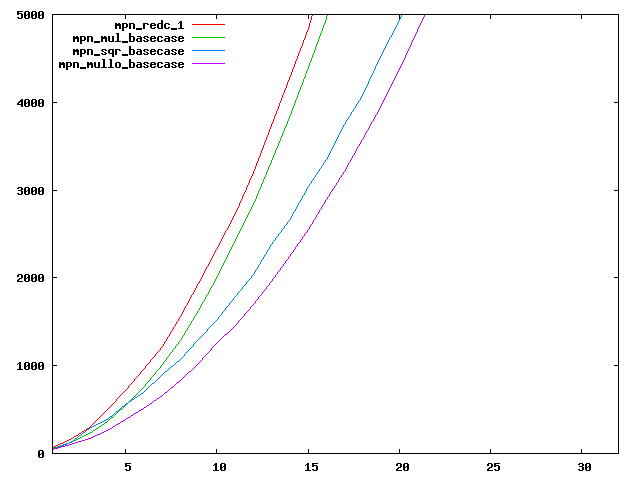
We are working to make critical basecase functions perform near-optimally on interesting CPUs. The current status can be seen in the diagrams below. The diagrams are ordered pairwise per CPU, with linear scale to the left and log/log scale to the right. Measured values are in cycles.
Well-formed functions should perform smoothly, where the order from slowest to fastest should be redc_1, mul_basecase, sqr_basecase, and mullo_basecase. In most cases where the order is not well-formed, assembly support is missing or inadequate.
The diagrams are sorted fastest-CPU-first as measured by mul_basecase, except that Itanium and POWER7 are at the end. The diagrams' ranges are the same for all CPU types, to allow some vertical comparisons.
| Intel Haswell lin/lin | Intel Haswell log/log |
|---|---|
 |  |
| AMD K10/Thuban lin/lin | AMD K10/Thuban log/log |
 | 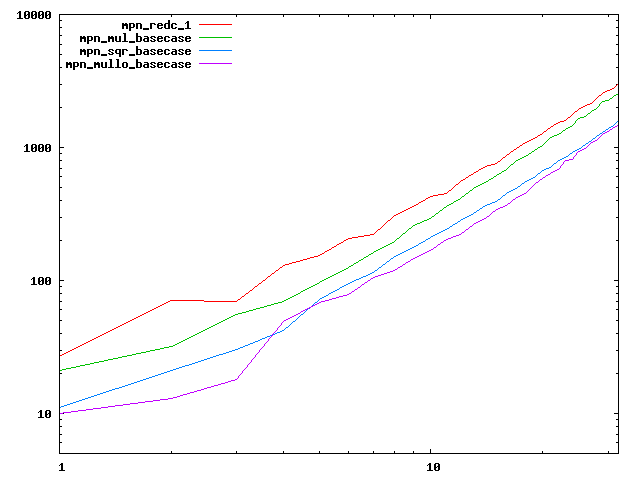 |
| Intel Ivy bridge lin/lin | Intel Ivy bridge log/log |
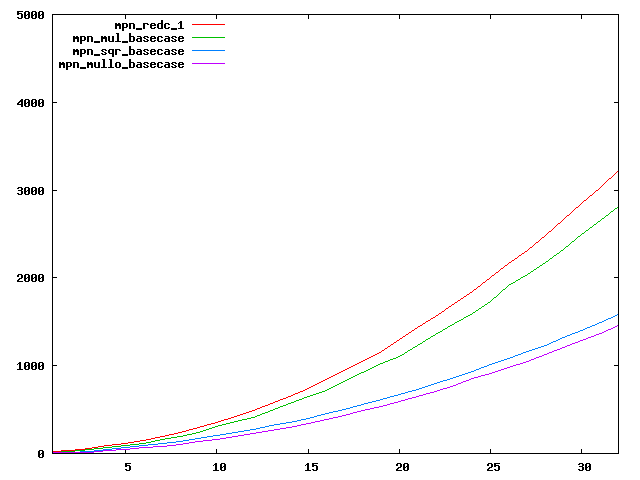 | 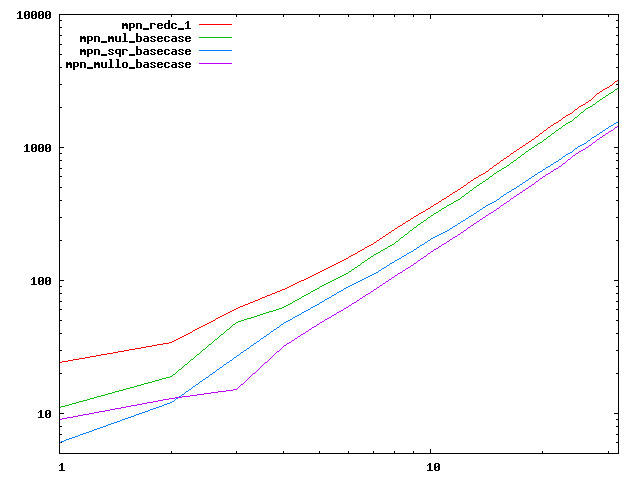 |
| Intel Sandy bridge lin/lin | Intel Sandy bridge log/log |
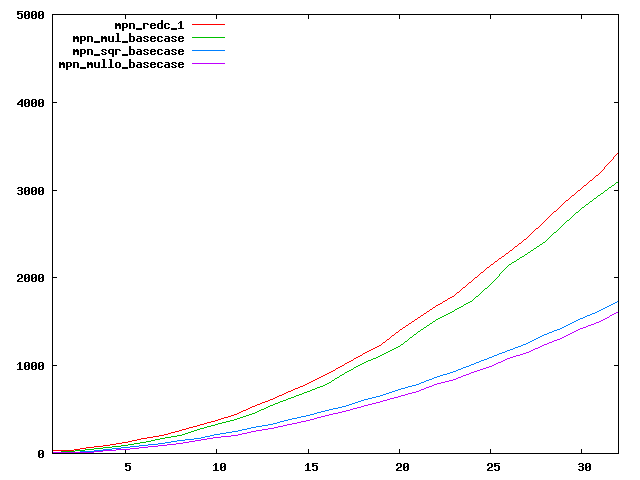 | 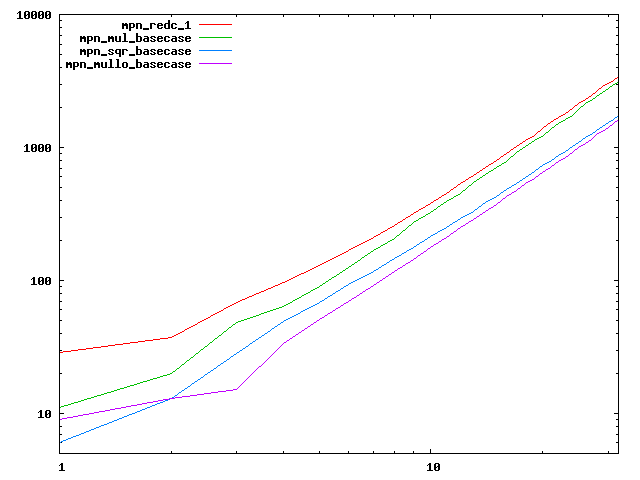 |
| Intel Nehalem lin/lin | Intel Nehalem log/log |
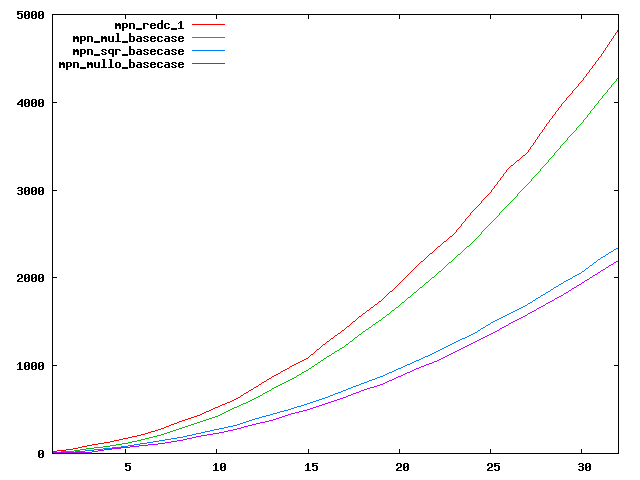 | 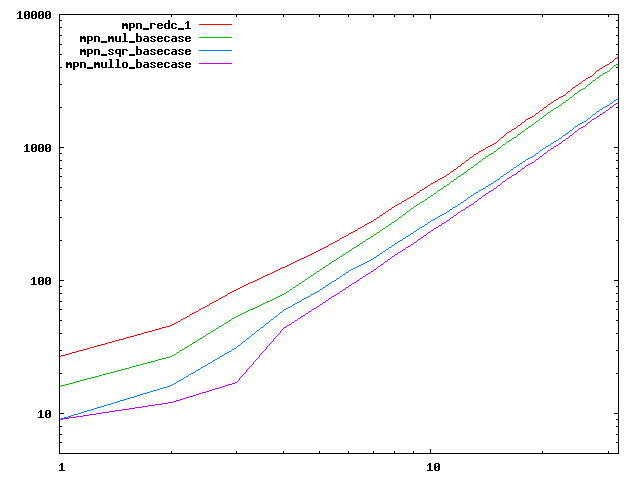 |
| Intel Conroe lin/lin | Intel Conroe log/log |
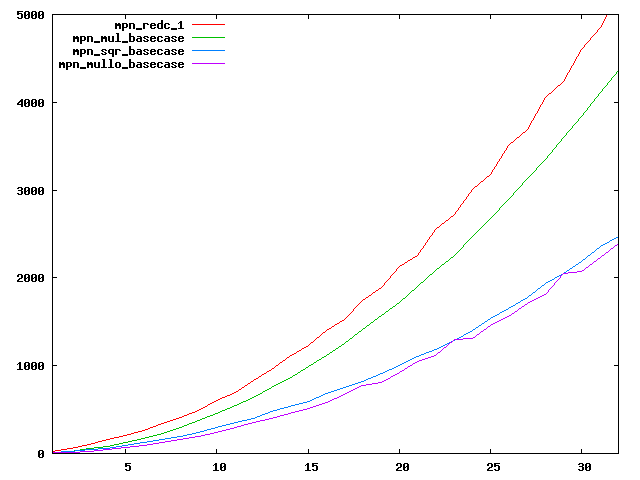 | 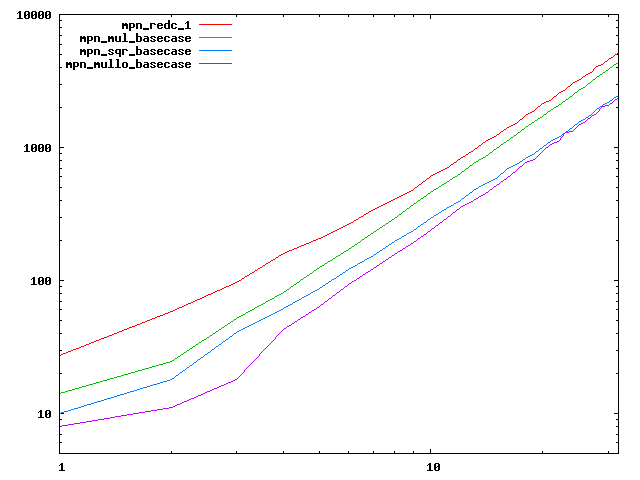 |
| AMD Piledriver lin/lin | AMD Piledriver log/log |
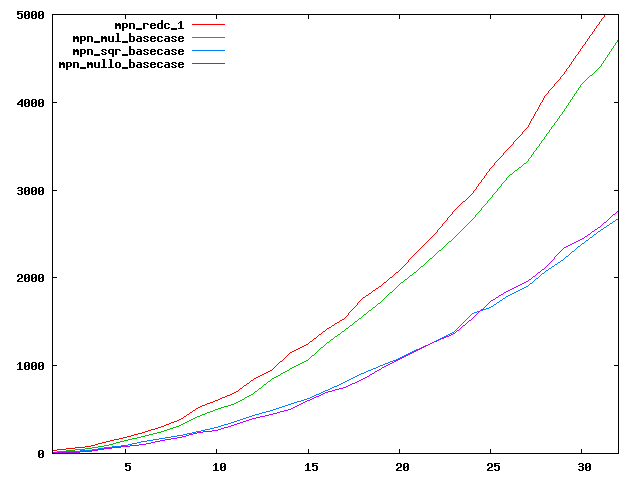 | 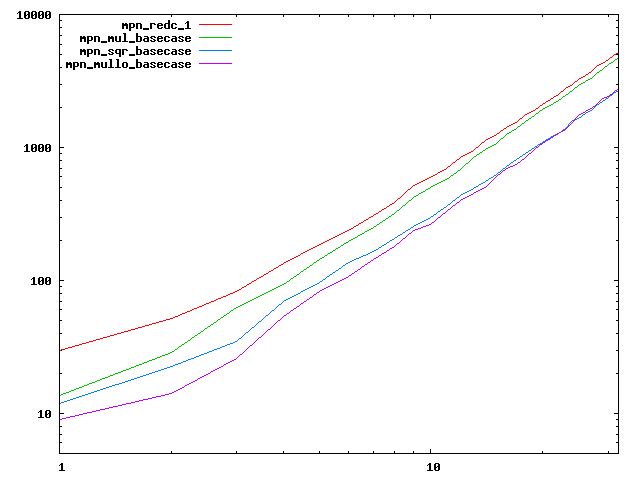 |
| AMD Bulldozer lin/lin | AMD Bulldozer log/log |
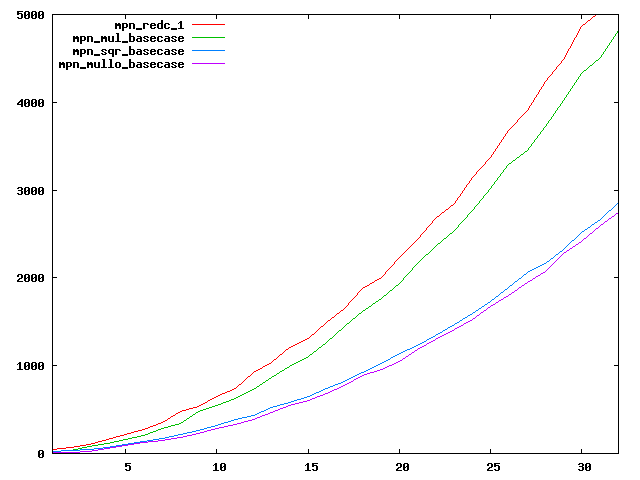 | 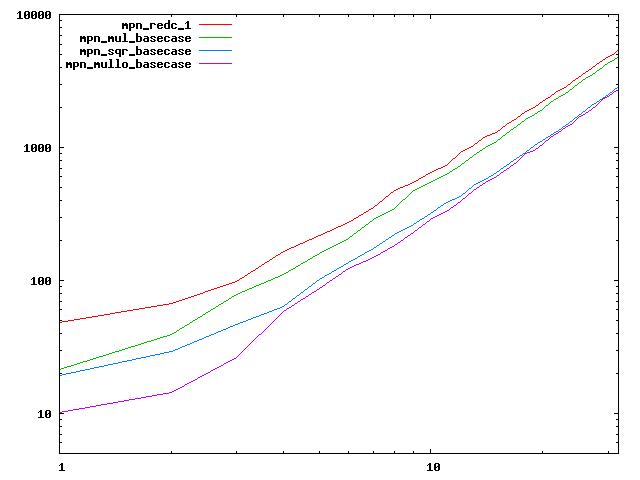 |
| AMD Bobcat lin/lin | AMD Bobcat log/log |
 | 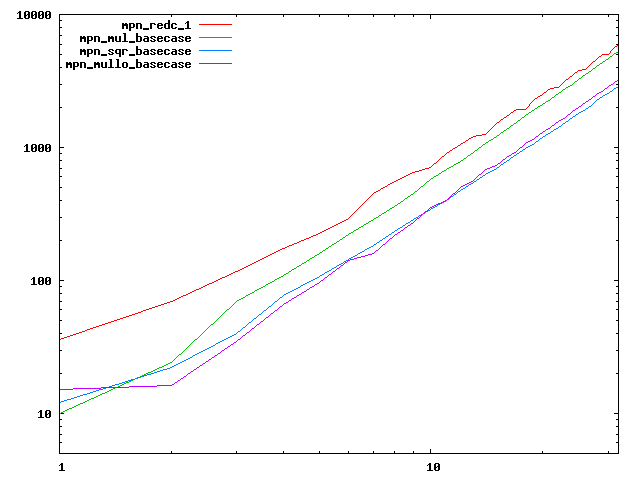 |
| Intel Atom lin/lin | Intel Atom log/log |
 | 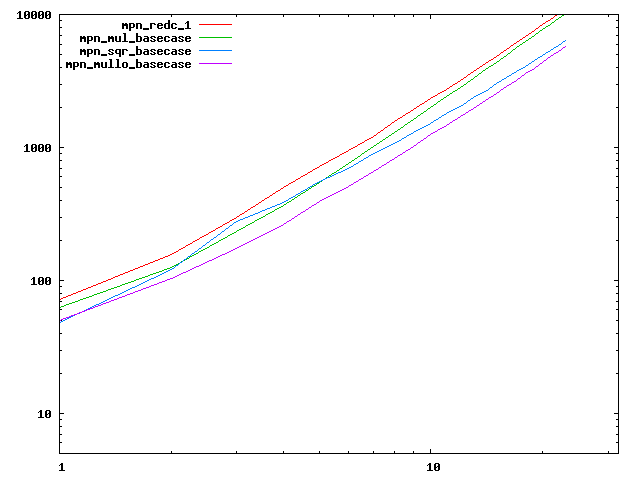 |
| Intel Itanium2 lin/lin | Intel Itanium2 log/log |
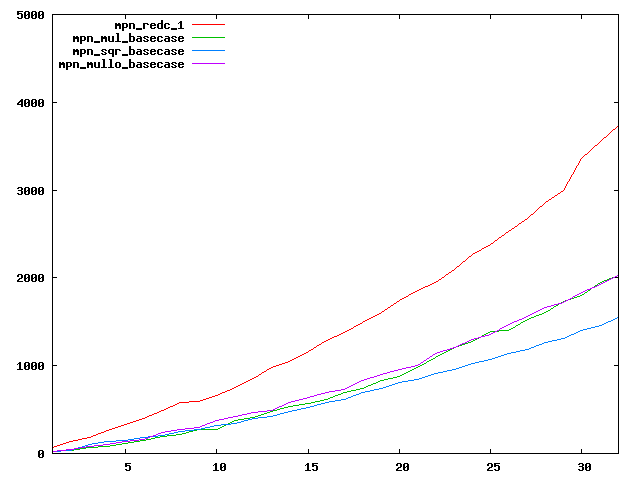 | 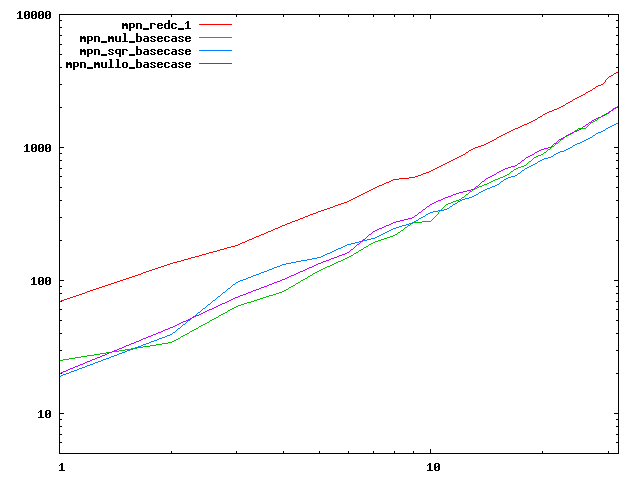 |
| IBM POWER7-smt4 lin/lin | IBM POWER7-smt4 log/log |
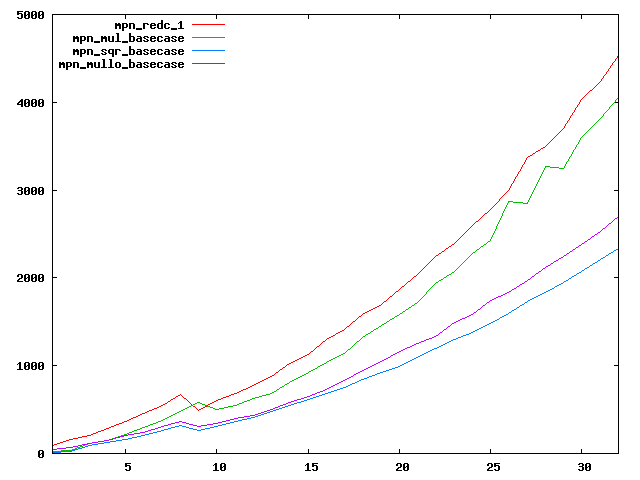 | 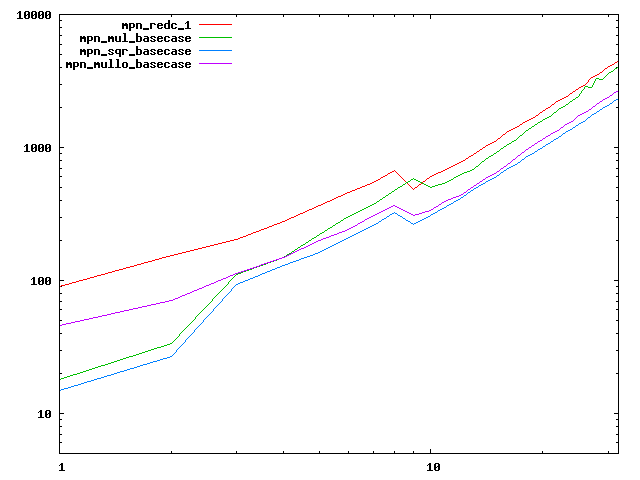 |
Division performance anomalies (mostly obsolete with 6.0.0)
These diagrams show performance for fixed quotient sizes, meaning that the difference between the dividend size and the divisor size is constant. The quotient size can be deduced from the "new-10000", "new-11365", etc. The x-axis is the dividend size. The red line is for the code up until GMP 5.1, the green line is new code. The new code uses more memory, but is almost always faster. Click for larger diagrams.
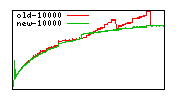
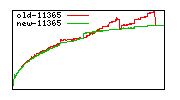
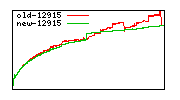
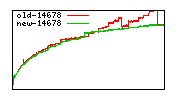
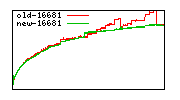
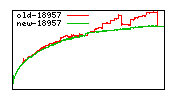
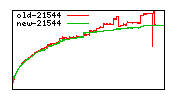
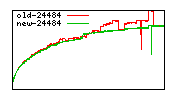
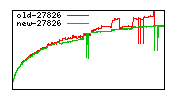

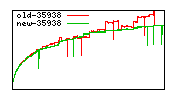
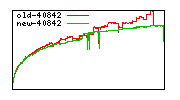
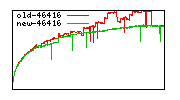
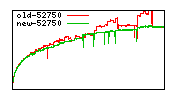
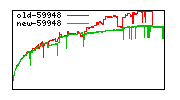
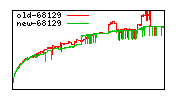
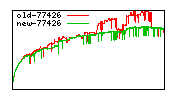
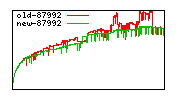
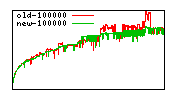
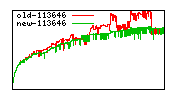
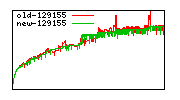
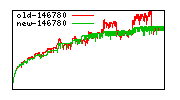
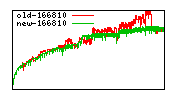
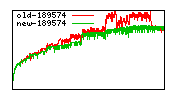
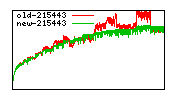
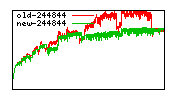
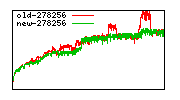
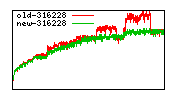
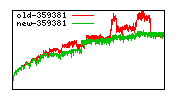
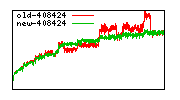
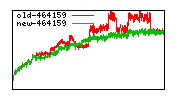
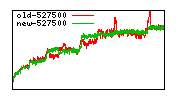
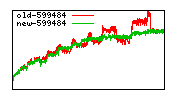
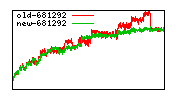
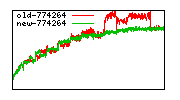
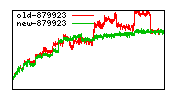
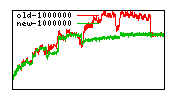
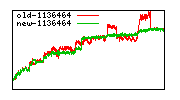
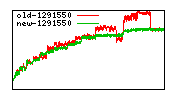
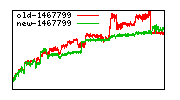
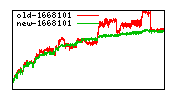
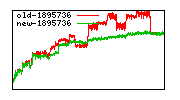
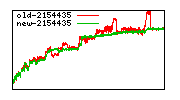
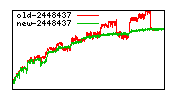
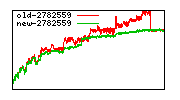
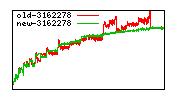
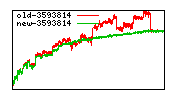
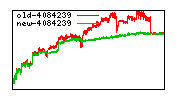
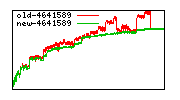
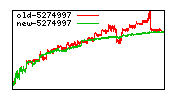
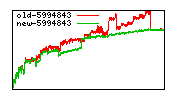
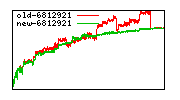
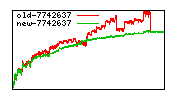
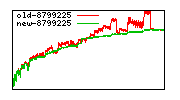
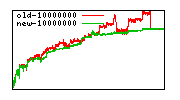
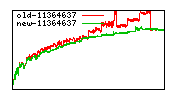
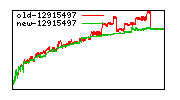
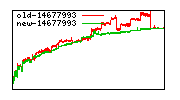
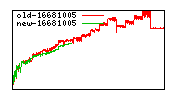
mpz_powm and mpz_powm_ui
This is a suggested new algorithm (in simple square-and-multiply form, in practice we should use k-ary sliding window):
// Compute r ← be mod m, m odd, e ≥ 2.
// Optimised for the case b << m. The first loop avoids reductions,
// the alternate 2nd loops performs necessary reductions.
// Let β be the word base and let n = ⌈logβ m⌉
r ← b
while 2 × logβ r < logβ m
r ← r2
if next-lower-bit(e) = 1
r ← r × b
if no-more-bits(e)
return r (mod m) // mod sometimes needed
if few-bits-remaining-in(e) ∨ ⌈logβ b⌉ + 3 < ⌈logβ n⌉
while true
r ← r2 mod m
if next-lower-bit(e) = 1
r ← r × b mod m
if no-more-bits(e)
return r
else
r' ← β^n × r mod m // convert to REDC residue
b' ← β^n × b mod m // convert to REDC residue
mi ← m-1 mod βk // a suitable modular inverse
while true
r' ← REDC((r')2, m, mi)
if next-lower-bit(e) = 1
r' ← REDC(r' × b', m, mi)
if no-more-bits(e)
return REDC(r', m, mi)
endif
New division interface
We are working in a modernised set of low-level division loops, splitting several of the current functions that have multiple loops into separate functions. Here we will try to describe the progress.
The function naming scheme is not completely coherent, and is far from finalised.
symbol meaning 1n,2n function expects normalised divisor, 1 and 2 limbs respectively 1u,2u function expects unnormalised divisor, 1 and 2 limbs respectively ; delimiter between output and input operands qp, np, dp pointers to quotient, numerator, and divisior qh high quotient limb d divisor limb r remainder limb di some sort of inverse of divisor
Euclidian division/mod by a 1-limb divisor function int function frac r = mpn_div_qr_1n_pi1(qp,qh;np,nn,d,di) r = mpn_divf_qr_1_pi1(qp;fn,r,d,di) r = mpn_div_qr_1u_pi1(qp,qh;np,nn,d,di) r = mpn_div_qr_1n_pi2(qp,qh;np,nn,d,di) r = mpn_divf_qr_1_pi2(qp;fn,r,d,di) r = mpn_div_qr_1u_pi2(qp,qh;np,nn,d,di) r = mpn_div_r_1n_pi1(;np,nn,d,di) r = mpn_div_r_1u_pi1(;np,nn,d,di) r = mpn_div_r_1n_pi2(;np,nn,d,di) r = mpn_div_r_1u_pi2(;np,nn,d,di)
Euclidian division/mod by a 2-limb divisor function int function frac qh = mpn_div_qr_2n_pi1(qp,rp[2];np,nn,dp[2],di) mpn_divf_qr_2n_pi1(qp;fn,np[2],dp[2],di) qh = mpn_div_qr_2u_pi1(qp,rp[2];np,nn,dp[2],di) qh = mpn_div_qr_2n_pi2(qp,rp[2];np,nn,dp[2],di) mpn_divf_qr_2n_pi2(qp;fn,np[2],dp[2],di) qh = mpn_div_qr_2u_pi2(qp,rp[2];np,nn,dp[2],di) mpn_div_r_2n_pi1(rp[2];np,nn,dp[2],di) mpn_div_r_2u_pi1(rp[2];np,nn,dp[2],di) mpn_div_r_2n_pi2(rp[2];np,nn,dp[2],di) mpn_div_r_2u_pi2(rp[2];np,nn,dp[2],di)
Euclidian division/mod by an m-limb divisor function mpn_div_qr mpn_div_qr mpn_div_q mpn_div_q mpn_div_r mpn_div_r
Euclidian mod by a 1-limb divisor function mpn_mod_1_1p mpn_mod_1s_2p mpn_mod_1s_3p mpn_mod_1s_4p
Hensel division/mod by a 1-limb divisor function mpn_bdiv_qr_1_pi1 mpn_bdiv_qr_1_pi2 mpn_bdiv_r_1_pi1 mpn_bdiv_r_1_pi2
Hensel division/mod by a 2-limb divisor function mpn_bdiv_qr_2_pi1 mpn_bdiv_qr_2_pi2 mpn_bdiv_r_2_pi1 mpn_bdiv_r_2_pi2
Hensel division/mod by an m-limb divisor function mpn_bdiv_qr mpn_bdiv_qr mpn_bdiv_q mpn_bdiv_q mpn_bdiv_r mpn_bdiv_r
Hensel mod/redc function mpn_redc_1 mpn_redc_2 mpn_redc_n
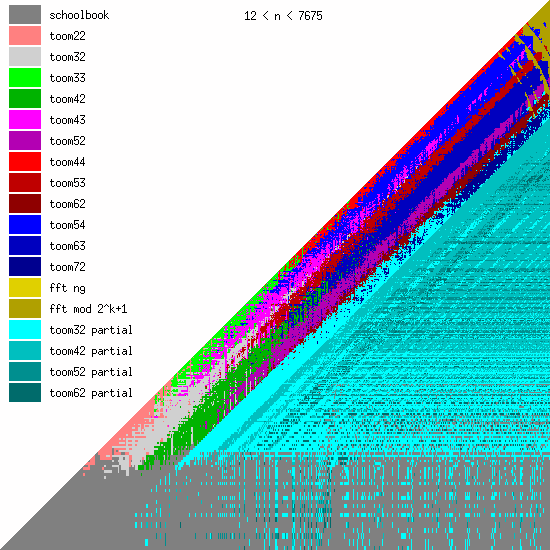
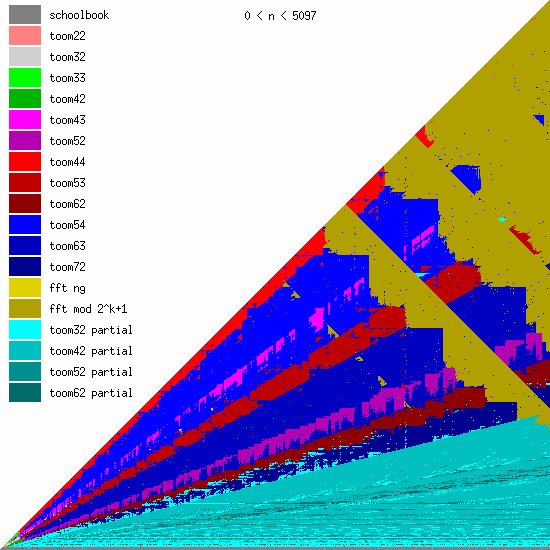
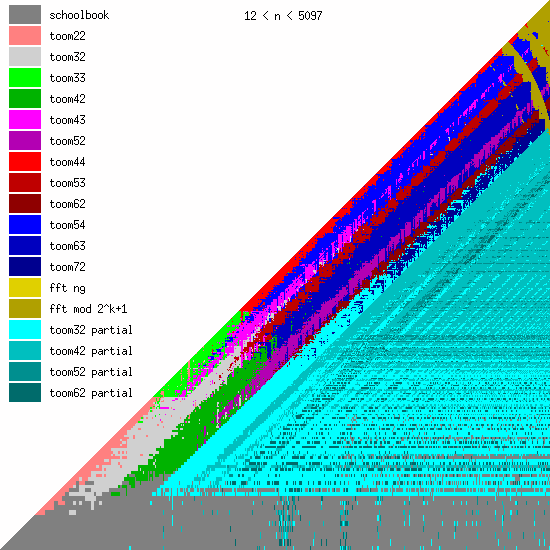
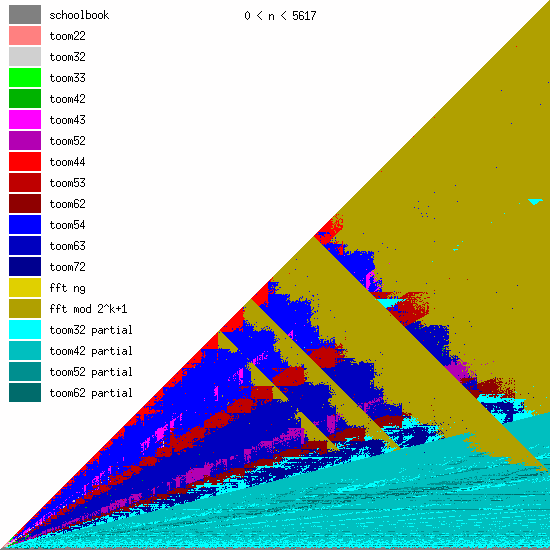
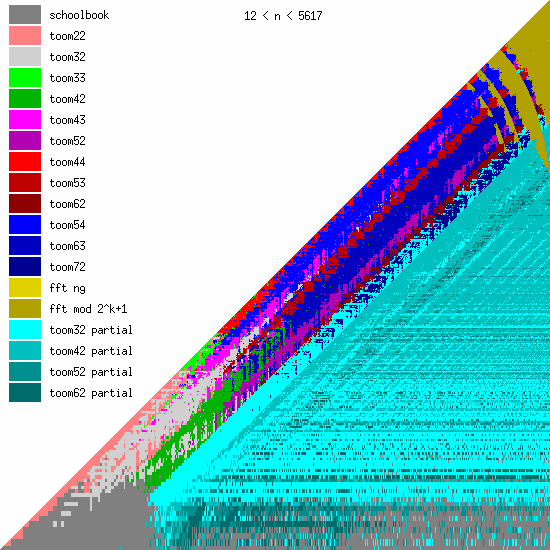
New Toom multiplication code for unbalanced operands
We have been adding more Toom functions during the last years, mainly for better handling of unbalanced operands.
We believe that even more Toom functions might be needed for optimal performance, probably going further than 8 evaluation points (used by toom54, toom63, toom72). This will largely depend on ongoing work on FFT multiplication; the faster that will become, the less room for higher-order Toom. The large number of functions is a bit disturbing, of course, since complexity is always bad. (But performance is GMP's main objective.)
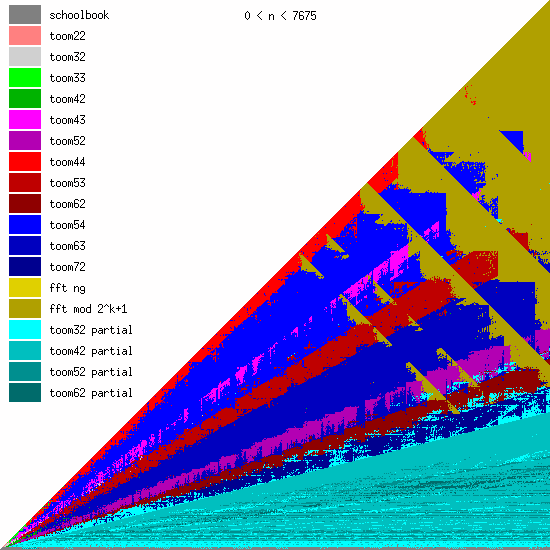
These pictures show the best current multiplication primitive for operand sizes 1 ≤ bn ≤ an ≤ N limbs, where N is indicated in each diagram. The x-axis represents an, which is the size of the first operand; the y-axis represents bn, the size of the second operand. The first picture uses linear scale, the second uses log/log scale. For larger scale, click the pictures.
Comments:
- GMP 4.3 uses schoolbook, toom22, toom32, toom42, toom33, toom44, and FFT.
- GMP 5.0 also uses toom43, toom53, and toom63, and the algorithm selection code for unbalanced operands has been improved.
- FFT takes over for larger operands for machines with faster hardware multiplication. AMD's processors have great hardware multiplication, Intel's Nehalem's multiplication has twice Athlon's latency, and the venerable Pentium 4 has really poor hardware multiplication. Basecase (a k a schoolbook) multiplication performance is direct function of hardware multiplication performance. And since the various Toom functions recurse into a large number of smaller basecase function invocations, their performance is also very linked. But FFT performs most of its work doing shifts and additions, and while these are also faster on Athlons, the other processors are closer behind.
| 
|
| 
|
| 
|
The ideas behind much of the Toom multiply improvements are due to Marco Bodrato and Alberto Zanoni. Please see Marco Bodrato's site for more information about Toom multiplication. The algorithmic foundation was made by Anatolii Alexeevitch Karatsuba in 1962, and Andrei Toom in 1963. The GMP implementations were made by Marco Bodrato, Niels Möller, and Torbjörn Granlund.
This tool is useful for for optimising the evaluation sequences of Toom functions. It exhaustively searches for possible sequences, given a goal function. It is similar to the GNU superoptimizer, except that this program optimises over a a simple algebraic structure and handles m-ary -> n-ary projections (the GNU superoptimizer optimises over an assembly language subset, and handles m-ary -> 1-ary projections). This is very immature code, but it seems to work.
Download files Last changed What changed? superopt-va.c 2007-01-16/2 speedup+UI improvement goal-va.def 2007-01-16 bug fixes